Macromolecular equilibria are classically modeled as transitions between fixed states. Protein folding, for example, has often been described as a two-state process, wherein the protein fluctuates between two discrete states, the native state and the unfolded (or denatured) state. This is a reasonable approximation of protein unfolding within the transition region (1), but does not adequately reflect the other equilibria that exist under strongly native conditions, where the unfolded state is highly unstable. Under such conditions, the equilibrium is dominated by states that are conformational excursions from the high-resolution structure as determined from hydrogen exchange and NMR relaxation data (2-32). To model this heterogeneity, COREX/BEST employs a particularly simple approach that recapitulates many of the observations of hydrogen exchange properties of proteins (33,34). This approach is based on an empirically derived parameterization of the relative free energy function describing each state (See below), and a simple scheme for an approximate but (hopefully) effectively accurate description of the ensemble of states. To achieve this approximate enumeration, the high-resolution structure of the protein is used as a template onto which a partitioning scheme is applied (Figure 1).

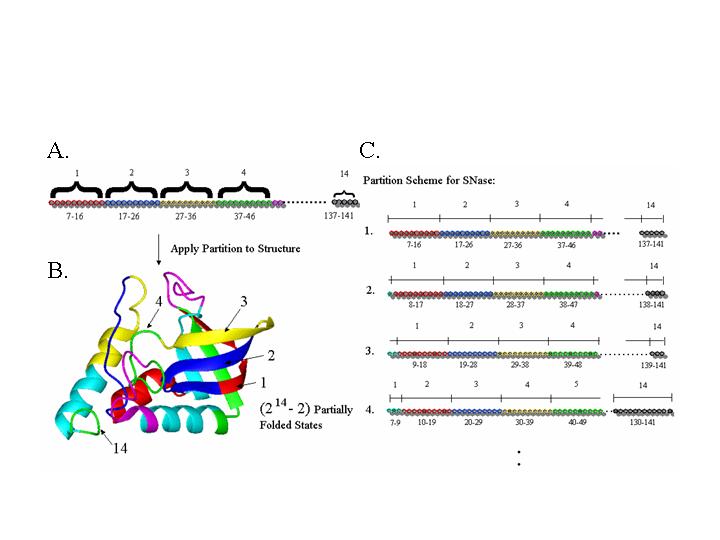
Figure 1:Limited enumeration of the protein ensemble. A. The linear sequence of the protein is partitioned into folding units. B. The folding units are applied to the three dimensional structure and all possible combinations of 'unfolded' and 'folded' states of each folding unit are created to define the ensemble. C. End effects are accommodated by sliding the folding units along the linear sequence.

Figure 1 shows the partitioning of staphylococcal nuclease (SNase) as an example. In this example a folding unit window size of 10 residues is employed. To begin the partitioning, the first ten residues are assigned to the first folding unit, the second ten are assigned to the second folding unit, and so on. The partitioning is then overlaid onto the high-resolution structure and an ensemble of states is generated by systematically assigning each folding unit as either fully folded (native) or fully unfolded. This produces 2^N-2 partially native states, representing all possible combinations. To examine the influence of the location of each partition, the partition boundaries are systematically varied by sliding the folding units one residue at a time in the sequence, and repeating the procedure described above.

Simplifying the Conformational Search

The approach outlined in Figure 1 represents an efficient and systematic means of distinguishing the regions of proteins that will be treated in the model as NATIVE-like from the regions that will be treated as NON-NATIVE-like. The crystal structure can be used to describe the NATIVE-like regions. The question then becomes, how should the NON-NATIVE regions be treated? Should alternative conformations be considered explicitly for each region? If so, how many? To estimate the magnitude of this problem, we need only realize that if 10 residues are to be treated as NON-NATIVE and each residue has 10 possible conformations, 10¹⁰ different conformations would have to be considered - an extremely large number to model explicitly. As fluctuations in multiple regions of the molecule must also be considered, it becomes clear that exhaustive structural enumeration is not a tractable solution.

To avoid the computational intractability of exhaustive enumeration, as well as the approximation of considering only a minute fraction of the relevant states, the COREX/BEST approach treats the fluctuations in statistical thermodynamic rather than structural terms. This is a key aspect of the approach. Using Boltzmann's equation,

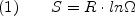
where S is the entropy, the symbol Omega is the number of conformations, and R is the gas constant, it is possible to estimate the energetic impact of all the conformational variants, provided an estimate of the number of possible conformational variants is known or can be calculated. In the context being used here, Equation 1 corresponds to the conformational entropy (S_conf) of the protein. Although this approach does not provide explicit structural details of the alternative conformations, it does address the thermodynamic impact of the entire ensemble, and thus can be considered rigorous from a statistical thermodynamic standpoint. In COREX/BEST, the residue specific Sconf values determined by the Freire lab are used (35,36) to consider the impact of unfolding isolated pieces of the protein in the context of an otherwise folded molecule.

2.

Defining the Relative Free Energy of Each State

Within the context of the ensemble representation of the energy landscape, once a particular state is identified, it is a straightforward matter to quantify the energetic contribution of that state to the overall properties of the ensemble. For each state, the statistical weight can be expressed as:

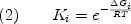
where R is the gas constant, T is absolute temperature, and deltaG_i is the Gibbs free energy of state i. deltaG_i can be further divided into the component enthalpy (deltaH_i) , entropy (deltaS_i) and heat capacity (deltaCp_i) contributions. Under the assumption of a temperature-independent deltaCp_i, and use of a reference temperature (T_ref), leads to the familiar Gibbs-Helmholtz expression:

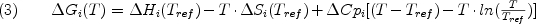
The importance of equation 2 is that the sum of the statistical weights of all N states in the ensemble corresponds to the partition function:

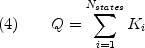
from which all important thermodynamic quantities, in particular the probability of each state, can be determined;

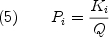
Equations (2) through (5) reveal that the rigorous formal description of the energies in the context of the ensemble representation is remarkably simple. Indeed, equation 3 reveals that calculating the free energy of each state requires estimates for the enthalpy, entropy, and heat capacity. To obtain these estimates we turn to the surface area based parameterization of Freire and co-workers (35-42).

Enthalpy and Heat Capacity

To determine the relative free energy of each state created by the partitioning scheme in Figure 1, a particularly simple deconstruction is employed. As is well known, the enthalpy and the heat capacity of unfolding proteins can be related to the difference in solvent-accessible surface between the high-resolution structure and unfolded state of the protein, assuming it is fully unfolded (Figure 2). The good agreement between the experimental and the calculated energetics in Figure 2 suggests that the thermodynamics of the partially folded states calculated by this approach will provide a reasonable approximation of the actual energetics. Most importantly, the energetics can be calculated and compared to experimental results under multiple environmental conditions, thus extending the scope of the experimental data that can be used to refine the model.

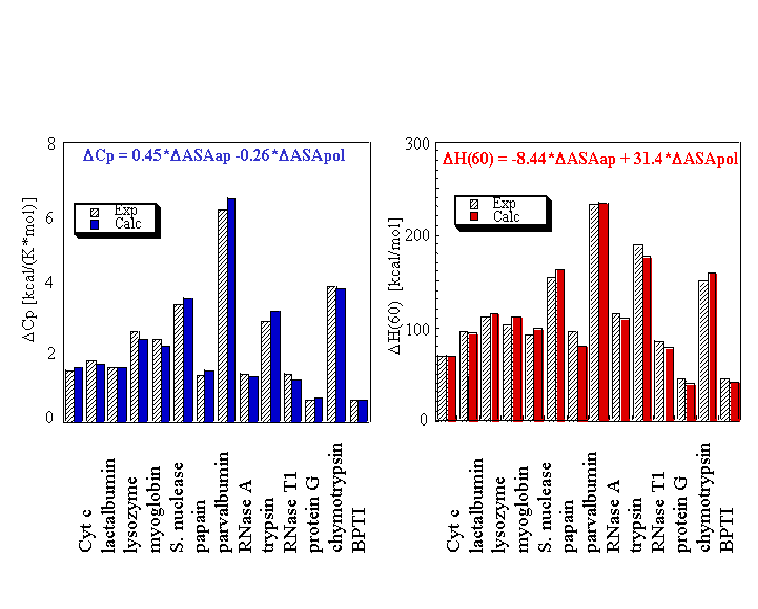
Figure 2: Parameterization of the heat capacity and enthalpy. Hashed bars show the calorimetrically obtained changes in heat capacity and enthalpy of unfolding for a database of proteins of various sizes. Colored bars represent those values for the heat capacity and enthalpy that are calculated using the parametric equations shown at the top of the graphs, which relate each quantity to the changes in solvent-accessible surface area upon unfolding (adapted from (Ref. 37 & 38)).

Entropy

The entropy difference between each state and a reference state can also be calculated for each state in the ensemble from parameterized energetics (35-42). Briefly, the entropy is divided into two components, solvent entropy (deltaS_solv) and conformational entropy (delta S_conf);

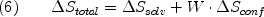
where W is entropy weighting (discussed below). The deltaS_conf represents the number of conformational variations that a particular energetic state can occupy. The important feature is that backbone and side chain conformational entropy values for each amino acid have been empirically determined as described above (35,36), thus providing a means of quantifying, in statistical thermodynamic terms, the conformational variability in the non-native segments of each state in the calculated ensemble shown in Figure 1. Although clearly a coarse approximation of the conformational space available to a particular protein segment, such an approach provides an efficient and systematic alternative to exhaustive enumeration.

As is the case with deltaH and deltaCp, the solvation entropy, deltaS_solv, is determined from changes in solvent-accessible surface area, which is calculated from the apolar and polar heat capacity contributions shown in Figure 2:

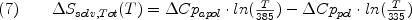
As is evident from the previous development, the description of each state, as well as the calculation of the energies provides only a coarse estimate. However, the advantage of this description is that it applies the same rule set to the generation of all states in the ensemble, regardless of how thermodynamically native or unfolded-like the state is. This approach therefore provides the ability to see the response of the ensemble as a whole to a perturbation.

Entropy Weighting (W)

The goal of the COREX/BEST is to investigate the structural and thermodynamic features of the conformational fluctuations that exist under native conditions. For most cases, these states are very native-like (i.e. mostly folded). However, COREX/BEST generates and determines the stability for a full spectrum of states, ranging from completely unfolded to completely folded, and it does so using the exact same set of rules for each state. A problem that emerges from this treatment is that uncertainty in a thermodynamic parameter will affect states that are structurally dissimilar to a greater extent than structurally similar states. For instance uncertainty in conformational entropy will affect unfolded states to a greater extent than more native-like states. We wish to be able to correct for the overall stability of the ensemble in a way that preserves the energetic hierarchy of native-like states. To do this, we consider the following development.

The energy function utilized in COREX/BEST is coarse and is designed to provide only a rough estimate (<~10%) of the thermodynamic parameters (i.e., deltaH, deltaCp, and deltaS) for each state. Because of this, the effects of ions, pH, ligands, and disulfides are treated in an approximate way (i.e. the energy function essentially averages these properties over all the proteins used to develop the structural energetic parameterization). To adjust for these time saving approximations in a way that does not impact the interpretation of the calculation, we employ a single adjustable parameter to each protein . This parameter, known as the entropy weighting (W), is multiplied with the calculated conformational entropy of each state in the ensemble.

The calculation of entropy in COREX/BEST involves a solvent, deltaS_solv, and a conformational, deltaS_conf, entropy term. Because deltaS_conf is on average proportional to the number of residues unfolded d, by adjusting the free energy of each state by an amount that is proportional to the number of residues unfolded (i.e. S_conf,Adj = W*S_conf), the ensemble is affected in a way that maintains the energetic hierarchy of states for a given degree of fraction native (Figure 3). For example, all states with Fraction Native of 0.8 are affected to approximately the same extent. Thus, the net effect of employing the entropy weighting (W) is to systematically shift the stability of the entire ensemble so that the left side of Figure 3 is either raised or lowered.

Although an entropy weighting can be calculated empirically by considering structural parameters such as the loop sizes created by disulfide bonds (43), or by considering the amount of exposed polar surface, these considerations only allow improved prediction of the overall stability (44). It is not clear that the stability calculation of each state is more accurate with such approaches. Because such treatments involve adding additional terms to the energy function, which increases computational demands and which are difficult to justify experimentally, we provide a means for users to apply their own entropy weighting. This entropy weighting can be derived directly from the known stability of the protein, or it can be calculated from more sophisticated user-derived software.

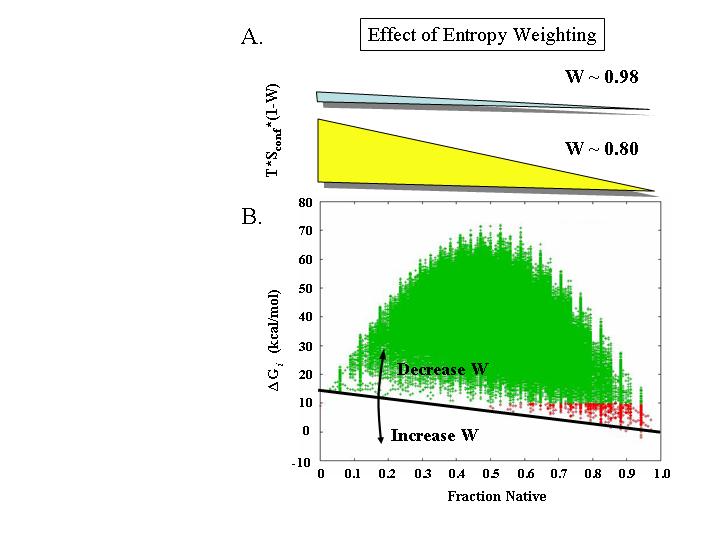
Figure 3: Effect of entropy weighting (W) on the different values of Fraction Native. On average, states with a given Fraction Native will have similar conformational entropies. A) The approximate energetic consequences of entropy weightings of 0.98 (i.e. 2% change) and 0.8 (i.e. 20% change) are shown for all the states in the Staphylococcal nuclease (SNase) ensemble (determined from PDB file 1STN). The thickness of the wedges are approximately scaled to the energies in B. B) Energetics of the SNase ensemble calculated with W = 0.998 (i.e. 0.2% change). Each point represents one state, and states are colored based on energy (green for deltaG > 10 kcal/mol; red for deltaG < 10 kcal/mol). Black line represents the relative effect of changing W (as shown in A) and arrows denote the direction of change.

From the probability of each state (Equation 5), any number of statistical thermodynamic descriptors of the equilibrium can be determined. One such quantity, known as the residue stability constant is the ratio of the summed probabilities of the states in the ensemble in which a particular residue is in a folded conformation (Pf,j), to the summed probability of the states in which a residue is in an unfolded conformation (Pnf,j);

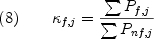
As equation 8 indicates residues with high stability constants will be folded in the majority of the highly probable states, and residues with low stability constants will be unfolded in many of the highly probable states. This is shown in figure 4, where the 30 of the low energy states of the staphylococcal nuclease ensemble is shown. Regions colored yellow in most states will have low stability constants, and regions colored red in those states will have high stability constants (33,34).

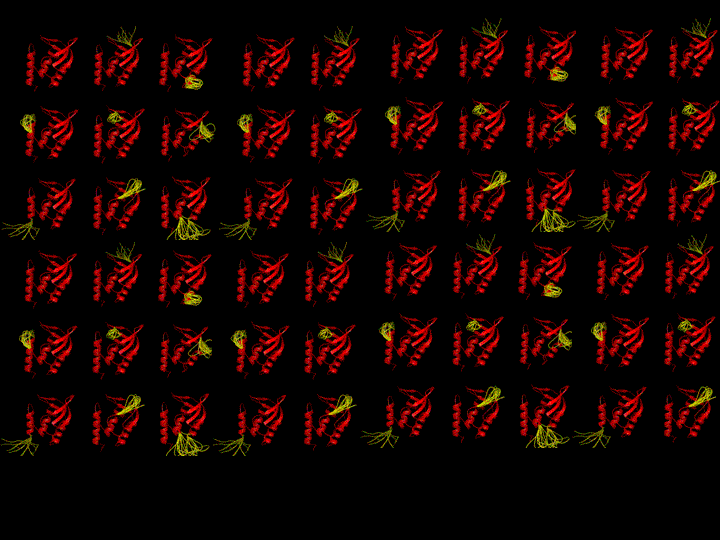
Figure 4.

Schematic representation of the low energy states in the staphylococcal nuclease conformational ensemble. Shown are 30 of the most probable states. Red denotes residues that are folded in each state, and yellow denotes residues that are unfolded. Multiple conformations shown for unfolded sections is for illustration purposes only, and is meant to convey that many possible conformations for unfolded sections are implicitly consider in the COREX/BEST algorithm. Note that the low energy states share common features. For instance the beta barrel is folded in all the ost probable states and the 40’s loop is unfolded in many of those states.

1. Lumry, R., Biltonen, R., and Brandts, J. F. (1966) Validity of the 'Two-State' Hypothesis for Conformational Transitions of Proteins.Biopolymers 4, 917-944.

2. Bai, Y, Sosnick, TR, Mayne, L, Englander, SW. (1995) Protein folding intermediates: Native-State Hydrogen Exchange. Science, 269,192+197.

3. Swint-Kruse, L. & Robertson, A. D. (1996). Temperature and pH dependences of hydrogen exchange and global stability for ovomucoid third domain. Biochemistry 35, 171+180.

4. Hvidt, A. & Nielsen, S. O. (1966). Hydrogen exchange in proteins. Adv. Protein Chem. 21, 287-386.

5. Kim, K.-S., Fuchs, J. A. & Woodward, C. K. (1993). Hydrogen exchange identifies native state motional domains important in protien folding. Biochemistry 32, 9600-9608.

6. Chamberlain, A. K., Handel. T. & Marqusee, S. (1996). Detection of rare partially unfolded molecules in equilibrium with the native conformation of RNase H. Nat. Struct. Biol. 3, 782-778.

7. Kim, K.-S. & Woodward, C. (1993). Protein internal flexibility and global stability: Effect of urea on hydrogen exchange rates of bovine pancreatic trypsin inhibitor. Biochemistry 32, 9609 9613.

8. Llinas, M., Gillespie, B., Dahlquist, F. W. & Marqusee, S. (1999). The energetics of T4 lysozyme reveal a hierarchy of conformations. Nat Struct Biol 6, 1072+1078.

9. Radford, S. E., Buck, M., Topping, K. D., Dobson, C. M. & Evans, P. A. (1992). Hydrogen exchange in native and denatured states of hen egg-white lysozyme. Proteins 14, 237-248.

10. Morozova, L. A., Haynie, D. T., Arico-Muendel, C., Van Dael, H. & Dobson, C. M. (1995). Structural Basis of the Stability of a Lysozyme Molten Globule. Nature Structural Biology 2, 871 875.

11. Woodward, C, Simon, I and Tuchsen, E. (1982) Hydrogen exchange and the dynamic structure of proteins. Molecular and Cellular Biochemistry, 48,135+160.

12. Van Dael, H., Haezebrouck, P., Morozova, L., Arico-Muendel, C. & Dobson, C. M. (1993). Partially Folded States of Equine Lysozyme. Structural Characterization and Significance for Protein Folding. Biochemistry 32, 11886+11894.

13. Loh, S. N., Prehoda, K. E., Wang, J. & Markley, J. L. (1993). Hydrogen exchange in unligated and ligated staphylococcal nuclease. Biochemistry 32, 11022+11028.

14. Itzhaki, L. S., Neira, J. L. & Fersht, A. R. (1997). Hydrogen exchange in chymotrypsin inhibitor 2 probed by denaturants and temperature. J. Mol. Biol. 270, 89-98.

15. Mayo, S. L. & Baldwin, R. L. (1993). Guanidinium chloride induction of partial unfolding in amide proton exchange in RNase A. Science 262, 873-876.

16. Woodward, C. K. & Rosenberg, A. (1971). Studies of hydrogen exchange in proteins. VI. Urea effects on ribonuclease exchange kinetics leading to a general model for hydrogen exchange from folded proteins. J. Biol. Chem. 246, 4114-4121.

17. Idiyatullin D. Nesmelova I. Daragan V.A.. Mayo K.H. (2003) Heat capacities and a snapshot of the energy landscape in protein GB1 from the pre-denaturation temperature dependence of backbone NH nanosecond fluctuations. J. Mol. Biol. 325, 149-62.

18. Alexandrescu, A.T., Rathgeb-Szabo, K., Rumpel, K., Jahnke, W., Schulthess, T., and Kammerer, R.A. (1998). 15N backbone dynamics of the S-peptide from ribonuclease A in its free and S-protein bound forms: Toward a site-specific analysis of entropy changes upon folding. Protein Sci. 7: 389-402.

19. Clore, G.M., Driscoll, P.C., Wingfield, P.T., and Gronenborn, A.M. (1990). Analysis of the Backbone Dynamics of Interleukin+1 ? Using Two-Dimensional Inverse Detected Heteronuclear 15N-1H NMR Spectroscopy. Biochemistry 29: 7387-7401.

20. Crump, M.P., Spyracopoulos, L., Lavigne, P., Kim, K.-S., Clark-Lewis, I., and Sykes, B.D. (1999). Backbone dynamics of the human CC chemokine eotaxin: Fast motions, slow motions, and implications for receptor binding. Protein Sci. 8: 2041-2054.

21. Farrow, N.A., Muhandiram, R., Singer, A.U., Pascal, S.M., Kay, C.M., Gish, G., Shoelson, S.E., Pawson, T., Forman-Kay, J.D., and Kay, L.E. (1994). Backbone Dynamics of a Free and a Phosphopeptide-Complexed Src Homology 2 Domain Studied by 15N NMR Relaxation. Biochemistry 33: 5984-6003.

22. Feher, V.A.and Cavanagh, J. (1999). Millisecond-timescale motions contribute to the function of the bacterial response regulator protein Spo0F. Nature 400: 289-293.

23. GagnéS.M., Tsuda, S., Spyracopoulos, L., Kay, L.E., and Sykes, B.D. (1998). Backbone and Methyl Dynamics of the Regulatory Domain of Troponin C: Anisotropic Rotational Diffusion and Contribution of Conformational Entropy to Calcium Affinity. J. Mol. Biol. 278: 667-686.

24. Kay, L.E., Torchia, D.A., and Bax, A. (1989). Backbone Dynamics of Proteins As Studied by 15N Inverse Detected Heteronuclear NMR Spectroscopy: Application to Staphylococcal Nuclease. Biochemistry 28: 8972-8979.

25. Lipari, G.and Szabo, A. (1982). Model-Free Approach to the Interpretation of Nuclear Magnetic Resonance Relaxation in Macromolecules. 2. Analysis of Experimental Results. J. Am. Chem. Soc. 104: 4559-4570.

26. Lipari, G.and Szabo, A. (1982). Model-Free Approach to the Interpretation of Nuclear Magnetic Resonance Relaxation in Macromolecules. 1. Theory and Range of Validity. J. Am. Chem. Soc. 104: 4546-4559.

27. Mandel, A.M., Akke, M., and Palmer, A.G. (1995). Backbone Dynamics of Escherichia coli Ribonuclease HI: Correlations with Structure and Function in an Active Enzyme. J. Mol. Biol. 246: 144+163.

28. Wagner, G. (1983). Characterization of the distribution of internal motions in the basic pancreatic trypsin inhibitor using a large number of internal NMR probes. Q. Rev. Biophys. 16: 1-57.

29. Wagner, G. (1995). The importance of being floppy. Struct. Biol. 2: 255-257.

30. Yang, D.W.and Kay, L.E. (1996). Contributions to conformational entropy arising from bond vector fluctuations measured from NMR-derived order parameters:application to protein-folding. J. Mol. Biol. 263: 369-382.

31. Ye, J., Mayer, K.L., and Stone, M.J. (1999) Backbone dynamics of the human CC-chemokine eotaxin. J. Biomol. NMR 15: 115+124.

32. Zidek L. Novotny M.V. Stone M.J (1999) Increased protein backbone conformational entropy upon hydrophobic ligand binding]. Nat. Struct. Biol. 6, 1118-21.

33. Hilser, V.J., and E. Freire. (1996) Structure Based Calculation of the Equilibrium Folding Pathway of Proteins. Correlation with Hydrogen Exchange Protection Factors. J. Mol. Biol. 262: 756-772.

34. Hilser, V.J., and E. Freire. (1997) Predicting the Equilibrium Protein Folding Pathway: Structure Based Analysis of Staphylococcal Nuclease.Proteins. 27: 171+183.

35. Lee, K.H., Xie, D., Freire, E., and Amzel, L.M. (1994) Estimation of changes in side chain configurational entropy in binding and folding: general methods and application to helix formation. Proteins 20, 68-84.

36. D'Aquino, J.A., Gomez, J., Hilser, V.J., Lee, K.H., Amzel, L.M., and Freire, E. (1996) The magnitude of the backbone conformational entropy change in protein folding. Proteins 25, 143-56.

37. Murphy, K.P.and Freire, E. (1992) Thermodynamics of structural stability and cooperative folding behavior in proteins. Adv Protein Chem 43, 313-61.

38. Freire, E.and Murphy, K.P. (1991) Molecular basis of co-operativity in protein folding. J Mol Biol 222, 687-98.

39. Luque, I., Mayorga, O.L., and Freire, E. (1996) Structure-based thermodynamic scale of alpha-helix propensities in amino acids. Biochemistry 35, 13681-8.

40. Hilser, V.J., Gomez, J., and Freire, E. (1996) The enthalpy change in protein folding and binding: refinement of parameters for structure-based calculations. Proteins: Struct. Funct. Genet. 26, 123-33.

41. Gomez, J., Hilser, V.J., Xie, D., and Freire, E. (1995) The heat capacity of proteins. Proteins: Struct. Funct. Genet. 22, 404+12.

42. Murphy, K.P., Xie, D., Thompson, K.S., Amzel, L.M., and Freire, E. (1994 ) Entropy in biological binding processes: estimation of translational entropy loss. Proteins 18, 63-7.

43. Pace, C.N., Grinsley, G.R., Thomson, J.A., and Barnett, B.J. (1988) Conformational stability and activity of ribonuclease T1 with zero, one and two intact disulfide bonds. J. Mol. Biol. 263, 11820-11825.

44. Hilser, V.J., Townsend, B.D., and E. Freire. (1997) Structure-Based Statistical Thermodynamic Analysis of T4 Lysozyme Mutants: Structural Mapping of Cooperative Interactions. Biophys. Chem. 64; 69-79.